2025/9/1 (更新日:2025/8/14)
高電圧の三相交流回路の送電線路における線路容量性・誘導性リアクタンスによる電圧降下の考え方【中級者用】

三相交流回路の受電端の電圧は実際にどうなるのでしょうか?
電力を送電する三相交流回路には、配線に容量性能や誘導性能があります。
送電線の特性を等価回路にして、受電端の電圧が生じる理論を解析します。
三相交流回路の受電端電圧を必要な電圧範囲に制御する方法が理解できるように説明していきます。
目次
- 送電線路で電圧降下が発生する原理
- 受電端電圧が送電端電圧より高くなる現象と原理
- 線路に存在するリアクタンス・アドミタンスの場合
1.送電線路で電圧降下が発生する原理

通常負荷の場合の、送電端電圧、受電端電圧、線路電流などの関係を整理します。
1-1. 等価回路
送電線の等価回路
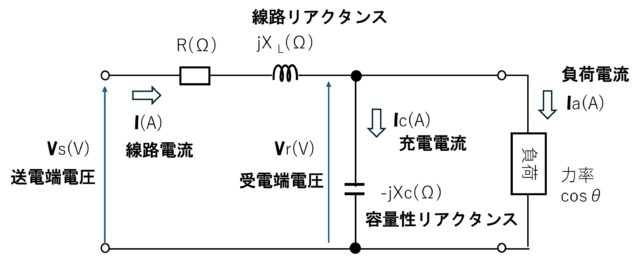
等価回路上の変数の意味
Vr:受電端の電圧
Vs:送電端の電圧
I:配線に流れる電流
Ic:容量性リアクタンスに流れる電流
Ia:負荷に流れる電流
jXL:配線に存在するリアクタンス
-jXc:配線に存在する容量性リアクタンス
R:配線の抵抗成分
cos θ:負荷の力率
1-2. 等価回路の考え方
負荷電流 Ia は、受電端電圧 Vr に対して負荷の位相角 θ 遅れになります。
また、容量性リアクタンスには、受電端電圧 Vr に対して 90度進みの充電電流 Ic が流れます。
線路に流れる、線路電流 I は、負荷電流と充電電流の和になります。
I = Ia + Ic
抵抗成分 R に電流 I が流れ、そこでの電圧降下は RI で電流 I と同相になります。
また、リアクタンス成分 XL には、90度 進みの電流が流れ、電圧降下は XL I になります。
受電端電圧に、抵抗成分、リアクタンス成分の電圧降下を加えたものが、送電端電圧になります。
Vs = Vr + RI + XLRI
1-3. ベクトル図
以上の関係をベクトルで表すと下記になります。
電圧・電流ベクトル図
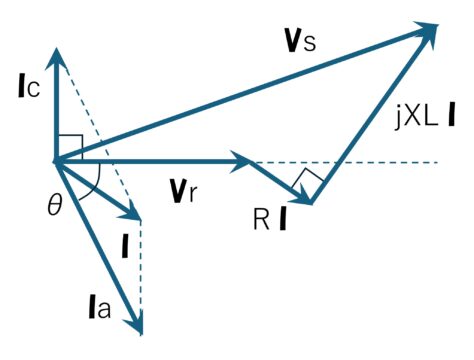
2.受電端電圧が送電端電圧より高くなる現象と原理

受電端電圧が送電端電圧より高くなる現象があります。
先に説明したベクトル図を基本に、軽負荷の場合の電圧と電流の関係を考えます。
電圧と電流の関係は負荷にかかわらず同じです。
軽負荷なので負荷電流【 I a 】が小さくなります。
充電電流【 I c 】の影響が大きくなり、線路電流が ”進み” になります。
その結果として、受電端電圧【 V r 】が送電端電圧【 V s 】より大きくなります。
電圧・電流ベクトル図
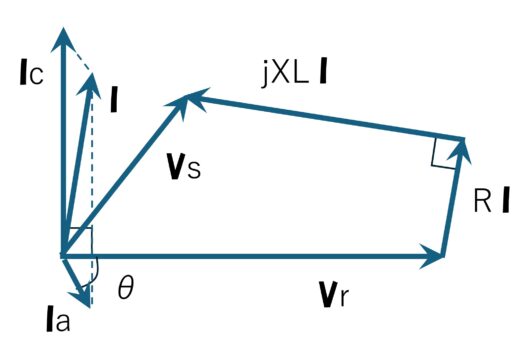
負荷が軽くなるほど進みの充電電流の影響が大きくなります。その結果、受電端電圧【 V r 】が送電端電圧【 V s 】より大きくなります。
この現象を、フェランチ効果と言います。
3.線路に存在するリアクタンス・アドミタンスの場合

線路電流が進み電流の場合、フェランチ効果が生じます。
実際の送電線でも、対地との間に静電容量が構成されてしまいます。
送電線の線路の付随する線路リアクタンス : X (Ω) と線路アドミタンス : B (S) の影響を考えます。
* アドミタンス B(S) は抵抗成分の逆数
また、配線抵抗は限りなく小さいので無視して考えます。
3-1. 等価回路
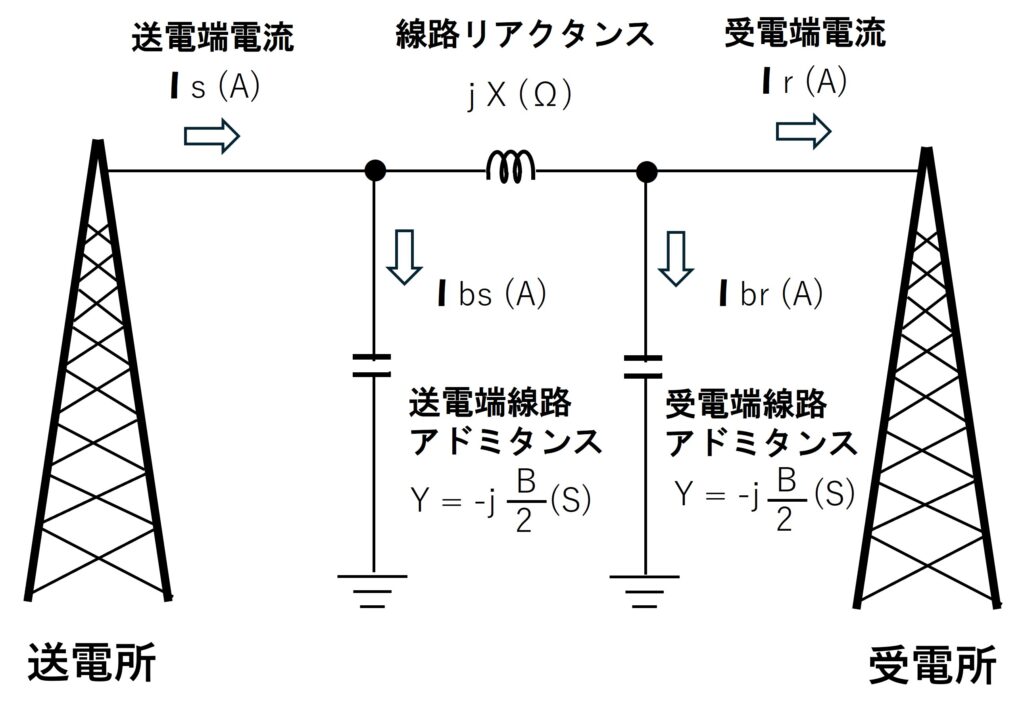
三相3線式の無負荷送電線の等価回路は下記になります。
送電線の等価回路
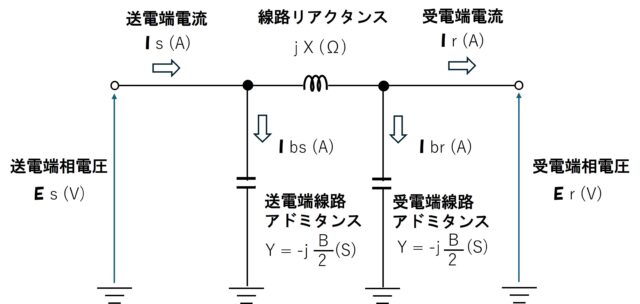
等価回路上の変数の意味
Er:受電端の相電圧
Es:送電端の相電圧
Is:配線に流れる送電端側の電流
Ibs:容量性リアクタンスに流れる送電端側の電流
Ibr:容量性リアクタンスに流れる受電端側の電流
Ir:配線に流れる受電端側の電流(負荷電流)
X:配線に存在するリアクタンス
Y:配線に存在する送電端側・受電端側のアドミタンス
この問題を解くにあたって、実体のイメージをしてください。
送電所から受電所に電気を送る想定します。
送電線はリアクタンスを持っていると同時に、対地との間に容量も存在します。
3-2. 等価回路の説明
無負荷を想定しているので、無負荷電流なので、I r = 0 A
受電端相電圧 E r = I br / ( j × B / 2) ⇒ I br = j × B × E r / 2
I br が E r より、位相が 90° 進んでいるのがわかります。
リアクタンス成分で生じる電圧は、
j × X × I br = j × X × ( j × B × E r / 2) = – X × B × E r / 2
リアクタンス成分で生じる電圧 j × X × I br は、受電端電圧 E r と、位相が180° ズレています。
送電端相電圧 E s = E r + ( j × X × I br ) = E r ( 1 – X × B / 2)
送電端相電圧 E s と 受電端相電圧 E r が、同相であることがわかります。
送電端側のアドミタンスから送電端相電圧 を求めます。
送電端相電圧 E s = I bs / ( j × B / 2) ⇒ I bs = j × B × E s / 2 = j × B × ( 1 – X × B / 2) × E r / 2
I bs が 受電端相電圧 E r より、位相が 90° 進んでいるのがわかります。
送電電流 I s = I br + I bs = j × B × E r / 2 + j × B × ( 1 – X × B / 2) × E r / 2
I s = j × B × ( 2 – X × B / 2) × E r / 2
送電電流 I s が 受電端相電圧 E r より、位相が 90° 進んでいるのがわかります。
3-3. 軽負荷時のベクトル図
以上をまとめて、ベクトル図で表します。
電圧・電流ベクトル図
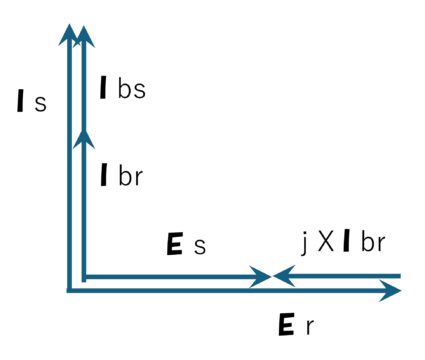
電圧及び電流のベクトル関係から明確にわかるように、
限りなく負荷が軽い無負荷の状態では、受電端相電圧 Er が送電端相電圧 Es より大きくなります。
4.まとめ

送電線路での電圧降下の仕組みについて解説しました。
基礎知識として少しでも参考にしてもらえれば幸いです。
最後まで読んでいただきありがとうございます。
説明できる内容は限られていますが、極力正確に伝えるように心がけました。
足りない部分、適切でない部分、補足などが有りましたらご指摘等お願いいたします。
Copyright–Seiji Nakamura, 2025 All Rights Reserved.












